Latitude and longitude, northing and easting, radius vector and polar angle—coordinates often come in pairs. However, that is not the whole story. A position is not adequately established until it is on a well-defined surface. This is where heights come in and since the primary sensor used today to determine positions is GPS/GNSS there are a few pertinent facts about heights that are worthwhile to know.
Any object in the Earth’s gravitational field has potential energy derived from being pulled toward the Earth. Quantifying this potential energy is one way to talk about height, because the amount of potential energy an object derives from the force of gravity is related to its height.
Here is another way of saying the same thing. The potential energy an object derives from gravity equals the work required to lift it to its current height. Imagine several objects, each with the same weight, resting on a truly level floor. In that instance, they would all possess the same potential energy from gravity. The floor on which they were resting could be said to be a surface of equal potential, an equipotential surface.
Now suppose that each of the objects was lifted up onto a level table. Their potential energies would obviously be increased in the process. Once they were all resting on the table their potential energies would again be equal, now on a higher equipotential surface, but how much higher?
There is more than one way to answer that question. One way is to find the difference in their geopotential, which is their potential energy on the floor, thanks to gravity, compared with their potential energy on the table. Another way to answer the question is to simply measure the distance along a plumb line from the floor to the tabletop. This latter method is the basic idea behind an orthometric height, the height that is most often desired. An orthometric height can be illustrated by imagining that the floor in the example is a portion of one particular equipotential surface called the geoid.
The geoid is a unique equipotential surface that best fits Mean Sea Level in a least squares sense. As you know, Mean Sea Level is not an equipotential surface at all because forces other than gravity affect it; temperature, salinity, currents, wind and etc. On the other hand, the geoid is defined by gravity alone. Therefore, it is lumpy as shown in this exaggerated illustration.
The geoid is lumpy because some parts of the Earth are denser than others, so gravity vectors do not all point in the same direction, nor do they have the same magnitude.
Now let’s look at a height that has no relationship to gravity at all, the type of height determined by a GPS/GNSS receiver unaided by a model of the geoid. Since the Earth closely resembles an oblate spheroid it can be, and often is, represented by a nice smooth mathematically defined reference ellipsoid.
The distance measured along a line perpendicular to the ellipsoid from the ellipsoid of reference to the surface of the Earth is called an ellipsoidal height. It is also known as a geodetic height and is usually symbolized, h. This is not the kind of height most often needed.
Fortunately an ellipsoidal height can be converted to an orthometric height if you know an essential distance sometimes known as a geoid height. It is also known as the separation and is usually symbolized, N. It is the distance measured along a line perpendicular to the ellipsoid from the ellipsoid of reference to the geoid. If the geoid is above the ellipsoid, N is positive if the geoid is below the ellipsoid, N is negative. Throughout the coterminous United States, sometimes abbreviated CONUS, the geoid is underneath the ellipsoid. The geoid heights vary from about -8 meters to about -53 meters from GRS80.
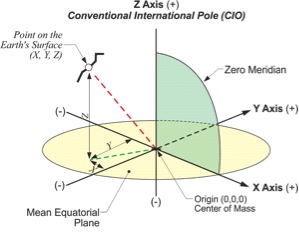
The orthometric height is most often symbolized, H. It is measured along a plumb line from the geoid to a point on the surface of the Earth. The relationship between these height related values is:
H= h – N
In summary, one can convert an ellipsoidal height (h) derived from a GPS/GNSS observation into an orthometric height (H) by knowing the extent of geoid-ellipsoid separation, the geoid height (N) at that point. Such information is available in models of the geoid which are freely available from the National Geodetic Survey (NGS) here: http://www.ngs.noaa.gov/GEOID/. The latest is GEOID 12A.
