A typical GPS/GNSS receiver unaided by a geoidal model will produce heights (aka elevations) that are measured from the ellipsoidal model of the Earth. These ellipsoidal heights are usually not the desired dimension. There is a long history and a good deal of legacy data that has been collected by differential spirit leveling. The resulting orthometric heights are by definition not ellipsoidal heights. They are measured from the geoid. It is unfortunate that these orthometric heights are quite often described as measured from Mean Sea Level (MSL). They are not.
Any object in the earth’s gravitational field has potential energy derived from being pulled toward the Earth. Quantifying this potential energy is one way to talk about height, because the amount of potential energy an object derives from the force of gravity is related to its height. There are an infinite number where the potential of gravity is always the same. They are known as equipotential surfaces.
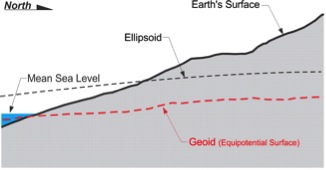
Mean Sea Level itself is not an equipotential surface at all, of course. Forces other than gravity affect it, forces such as temperature, salinity, currents, wind, and so forth. These unavoidable forces actually cause Mean Sea Level to deviate up to 1, even 2, meters from the geoid.
The geoid, on the other hand, is defined by gravity alone. The geoid is the particular equipotential surface arranged to fit Mean Sea Level as well as possible, in a least squares sense.
An often-used description of the geoidal surface involves idealized oceans. Imagine the oceans of the world utterly still, completely free of currents, tides, friction, variations in temperature and all other physical forces, except gravity. Reacting to gravity alone, these unattainable calm waters would coincide with the figure known as the geoid. Admitted by small frictionless channels or tubes and allowed to migrate across the land, the water would then, theoretically, define the same geoidal surface across the continents, too.
Of course, the 70% of the earth covered by oceans is not so cooperative, nor is there any such system of channels and tubes. In addition, the physical forces eliminated from the imagined ideal cannot be avoided in reality. These unavoidable forces actually cause mean sea level to deviate from the geoid. This is one of the reasons that Mean Sea Level and the surface of the geoid are not the same.
Gravity is not consistent across the topographic surface of the earth. At every point it has a magnitude and a direction. In other words, anywhere on the earth, gravity can be described by a mathematical vector. Along the solid earth, such vectors do not have all the same direction or magnitude, but one can imagine a surface of constant gravity potential. Such an equipotential surface would be level in the true sense. It would coincide with the top of the hypothetical water in the previous example. The vertical axis of any properly leveled surveying instrument and the string of any stable plumb bob are perpendicular to the geoid. Just as pendulum clocks and earth-orbiting satellites, they clearly show that the geoid is a reality.
The geoid does not precisely follow mean sea level, nor does it exactly correspond with the topography of the dry land. It is irregular like the terrestrial surface. It is bumpy. Uneven distribution of the mass of the planet makes it so. If the solid earth had no internal anomalies of density, the geoid would be smooth and almost exactly ellipsoidal. But like the earth itself, the geoid defies such mathematical consistency and departs from true ellipsoidal form by as much as 100 meters in places.
Ellipsoid–Geoid–Mean Sea Level
The geoid undulates with the uneven distribution of the mass of the earth. It has all the irregularity that the attendant variation in gravity implies. In fact, the separation between the lumpy surface of the geoid and the smooth GRS80 ellipsoid worldwide varies from about +85 meters west of Ireland to about -106 meters, the latter in the area south of India near Ceylon.
In the coterminous United States, sometimes-abbreviated CONUS, the distances between the geoid and the GRS80 ellipsoid, known as geoid heights, are less. They vary from about –8 meters to about –53 meters.
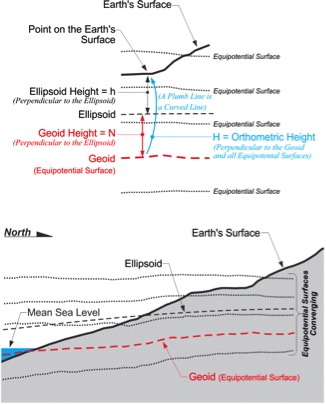
Height Conversion
A geoid height is the distance measured along a line perpendicular to the ellipsoid of reference to the geoid. Also, as you can see, these geoid heights are negative. They are usually symbolized, N. If the geoid is above the ellipsoid, N is positive; if the geoid is below the ellipsoid, N is negative. It is negative here because the geoid is underneath the ellipsoid throughout the coterminous United States. An orthometric height, symbolized, H, is measured along a plumb line from the geoid to a point on the surface of the earth. In either case by using the formula,
H = h – N
The current geoid model in place and available from the National Geodetic Survey (NGS) is known as GEOID12B