A spatial Cartesian system with three axes lends itself to describing the terrestrial positions derived from space-based geodesy. Using three rectangular coordinates instead of two, a person can unambiguously define any position on the earth—or above it for that matter. The three-dimensional Cartesian coordinates (x,y,z) derived from this system are known as Earth-Centered-Earth-Fixed (ECEF) coordinates. It is a right-handed orthogonal system that rotates with and is attached to the earth, which is why it is called earth fixed.
A three-dimensional Cartesian coordinate system is right-handed if it can be described by the following model: the extended forefinger of the right hand symbolizes the positive direction of the x-axis. The middle finger of the same hand extended at right angles to the forefinger symbolizes the positive direction of the y-axis. The extended thumb of the right hand, perpendicular to them both, symbolizes the positive direction of the z-axis.
But such a system is only useful if its origin (0,0,0) and its axes (x,y,z) can be fixed to the planet with certainty, something easier said than done.
The usual arrangement is known as the Conventional Terrestrial Reference System (CTRS), and the Conventional Terrestrial System (CTS). The latter name will be used here. The origin is the center of mass of the whole Earth including oceans and atmosphere, the geocenter. Thex-axis is a line from that geocenter through its intersection at the zero meridian, also known as the International Reference Meridian (IRM), with the internationally defined conventional equator. The y-axis is extended from the geocenter along a line perpendicular from the x-axis in the same mean equatorial plane toward 90° East longitude. That means that the positive end of the y-axis intersects the actual Earth in the Indian Ocean. In any case, they both rotate with the Earth around the z-axis, a line from the geocenter through the internationally defined pole known as the International Reference Pole (IRP).
However, the earth is constantly moving, of course. While one can say that the Earth has a particular axis of rotation, equator and zero meridian for an instant, they all change slightly in the next instant. Within all this motion how do you stabilize the origin and direction of the three axes for the long term? One way is to choose a moment in time and consider them fixed to the earth as they are at that instant.
Here is an example of that process of definition. The earth’s rotational axis wanders slightly with respect to the solid earth in a very slow oscillation called polar motion. The largest component of the movement relative to the earth’s crust has a 430-day cycle known as the Chandler period. It was named after American Astronomer Seth C. Chandler who described it in papers in the Astronomical Journal in 1891. Another aspect of polar motion is sometimes called polar wander. It is about 0.004 seconds of arc per year as the pole moves toward Ellesmere Island. The actual displacement caused by the wandering generally does not exceed 12 meters. Nevertheless, the conventional terrestrial system of coordinates would be useless if its third axis was constantly wobbling. Originally, an average stable position was chosen for the position of the pole. Between 1900 and 1905, the mean position of the earth’s rotational pole was designated as the Conventional International Origin (CIO) and the z-axis.
This was defined by the Bureau International de l’Heure (BIH). It has since been refined by the International Earth Rotation Service, (IERS) using very long baseline interferometry (VLBI) and satellite laser ranging (SLR). It is now placed as it was midnight on New Year’s Eve 1983, or January 1, 1984 (UTC). The moment is known as an epoch and can be written 1984.0. The name of the z-axis has been changed to the International Reference Pole, IRP epoch 1984, but it remains within 0.005” of the previous definition. It provides a geometrically stable and clear definition on the earth’s surface for the z-axis.
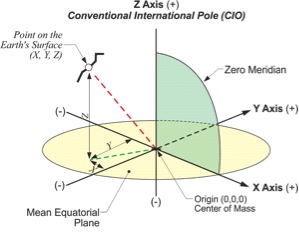
In this three-dimensional right-handed coordinate system the x-coordinate is a distance from the y-z plane measured parallel to the x-axis. It is always positive from the zero meridian to 90º W longitude and from the zero meridian to 90º E longitude. In the remaining 180º the X-coordinate is negative. The y-coordinate is a perpendicular distance from the plane of the zero meridian. It is always positive in the Eastern Hemisphere and negative in the Western Hemisphere. The z- coordinate is a perpendicular distance from the plane of the equator. It is always positive in the Northern Hemisphere and negative in the Southern Hemisphere.
It is important to note that the GPS Control Segment generates the position and velocity of the satellites themselves in ECEF coordinates. It follows that most modern GPS software provide the GPS positions in ECEF as well. Further, the ends of baselines determined by GPS observation are typically given in ECEF coordinates so that the vectors themselves become the difference between those x, y, and z coordinates. The display of these differences as DX, DY, and DZ is a usual product of these post-processed calculations.
